Il libro «Curve Policentriche – sistemi di raccordi tra archi e rette», si offre come strumento operativo nell’ostico campo delle tangenze tra i due tipi di linee, nel progettare, nel disegnare, nel fare design e nel realizzare manufatti. È soprattutto implicata la Geometria del piano, ma è anche lambita la tridimensione. Gli scenari identificati vanno dalle tecniche storicizzate, a quelle influenzate dal «digitale», come le lavorazioni a controllo numerico. La struttura di manuale non priva il gusto di una lettura speculativa e disinteressata.
Felice Ragazzo, è docente a contratto presso il CdL in Disegno Industriale, presso la Sapienza Università di Roma, ha redatto questo volume integrando i seguenti fattori:
• proposizioni euclidee, soprattutto relative ai cerchi;
• il «III lemma di Archimede»;
• le «Sezioni Coniche» come luoghi di equidistanza;
• il «Cerchio dei Raccordi», da egli stesso individuato.
Mettendo così a disposizione una metodologia semplice, rapida e sicura per tracciare archi e rette tangenti, anche in condizioni geometriche complicate. Tra i risultati ottenuti vi è quello della generalizzazione della tracciatura dell’ovale.
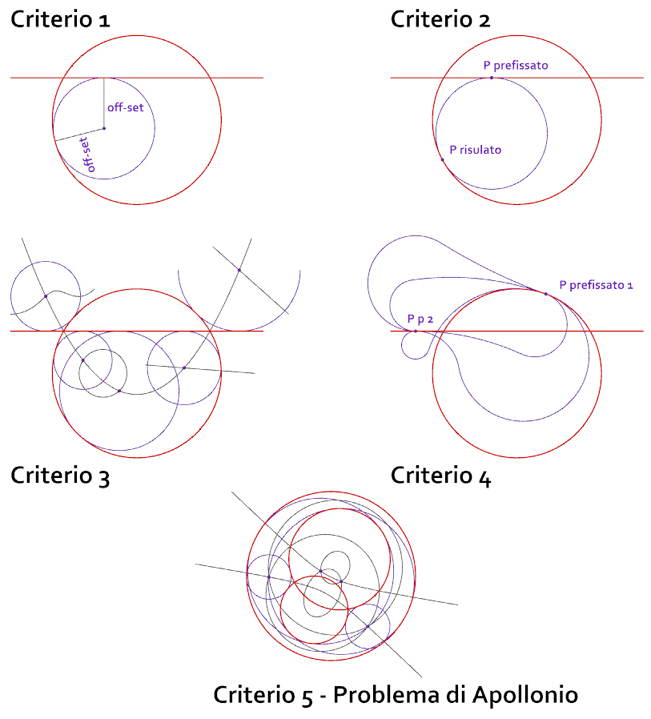
I criteri sviluppati sono cinque:
• uguale off-set delle curve da raccordare;
• fissare un punto su di un primo arco e raccordarlo con un secondo;
• fissare il centro del raccordo mediante l’intersezione tra il luogo di equidistanza tra archi o rette da raccordare e una curva qualsiasi;
• fissare su ciascun arco un punto di raccordo (in questo caso gli archi raccordanti sono necessariamente almeno due);
• raccordare tre curve date, archi e/o rette (Problema di Apollonio).
La presentazione è a cura del Prof. Franco Ghione.
La postfazione è a cura del Prof. Mario Docci.
Il libro si compone di 8 Capitoli e 4 Appendici.
I Capitoli 1-4 sono dedicati ad illustrare la teoria generale dei problemi implicati.
I Capitoli 5-8 sono dedicati ad illustrare i vari criteri trattati.
In maniera più o meno estesa, ogni Capitolo comprende una o più sezioni teoriche specifiche. La maggior parte dello spazio è occupata da esemplificazioni con l’intenzione di esaurire ogni casistica possibile.
L’Appendice 1 è dedicata alla supposizione di raccordo monocentrico tra curve non policentriche.
L’Appendice 2 è dedicata al III Lemma nell’ipotesi di una sua alterazione.
L’Appendice 3 è dedicata alla costruzione di un caso esemplare di “Sangaku“, il Teorema del Collare o di Soddy (otto sfere tangenti, inglobate in una nona tangente a tutte le altre).

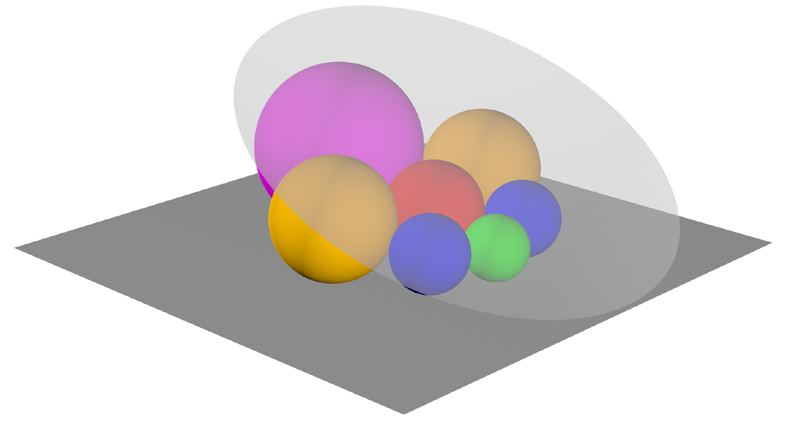
- in alto, la grande sfera incusiva ha raggio finito;in basso, la “sfera” inclusiva
- ha raggio infinito ed appare come un piano.
L’Appendice 4 è dedicata ad alcuni casi (architetture, dipinti, oggetti, etc.) in cui si suppone sussistano condizioni di tangenza tra archi e rette.
 Finestrone absidale nel Duomo di Milano.
Finestrone absidale nel Duomo di Milano.
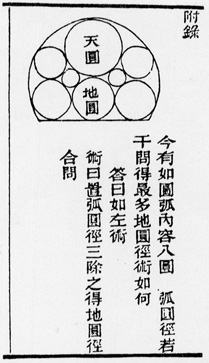
“Impacchettamento” di cerchi, dal “Suan Fa Yuan Li Kua Nang” (Sampo Enri Katsuno) di Kaetsu Denichiro (+1851), da L. Needam, Scienza e Civiltà in Cina, Torino, 1985, Einaudi, p. 130.
Copertine del libro


Prospettive Edizioni
Piazza Manfredo Fanti, 47
00185, Roma – tel. 06 97604531; 06 6875230
Direttore Arch. Claudio Presta
______________________________________________________________________________________________________________________________
Sul sito dell’Associazione per il Disegno Industriale www.adi-design.org, a cura di Dario Moretti – esperto di comunicazione e grande conoscitore dei fenomeni evolutivi del design oltre che di quelli più generali del costume – è stato postato un acuto commento proprio in riferimento al libro qui illustrato. Invito a cliccare il seguente link: https://www.adi-design.org/il-design-attraverso-le-curve.html al fine di poterlo leggere e apprezzare.
Un lusinghiero commento al libro è inoltre postato sul sito: https://matematica.unibocconi.it/libri/curve-policentriche a cura del Prof. Renato Betti – Emerito professore di Matematica presso il Politecnico di Milano.
